Counting organisms can be complex

Many times the problem of counting organisms in a population can be of great difficulty, in the case of organisms that we can identify as unitary it can result in less difficulty, but in modular organisms, such as corals, trees or others this problem can be of great relevance. Also at the moment of counting organisms and wanting to project the population into the future, we can find the problem that not all organisms are of the same category, there could be organisms that will never reach reproduction or organisms that have already passed their reproductive stage. However, despite all these points to take into consideration, models have been generated that seek to describe the dynamics of populations. In this example we will talk about the exponential growth model, a model independent of population density or density-independent. To illustrate it we will think of paramecia.

An initial model

Taking into account our population of paramecia this could grow due to them reproducing or because paramecia arrive from another population, that is to say from a birth rate ($B$) and immigration ($I$). On the other hand, our number of paramecia would decrease if some of these die or if they emigrate to another population, which we could consider a mortality rate ($D$) and an emigration rate ($E$), so the number of individuals in a future time, which we can denote as $t+1$, of a population would be given by the following:

That is to say, from the initial number of organisms, how many are born, how many die, how many immigrate and emigrate. To obtain the number of individuals in which the population changes between one time and another, we can write the following:

Now suppose we have a closed population, that is, it is not possible to emigrate from it or for immigrants to arrive, so our equation remains reduced to:

That is, the number of individuals only depends on how many are born and die. If we consider that our population of paramecia grows continuously, that is to say that it does not do so in time jumps, we can write the equation in differential form:

Where we can appreciate the infinitesimal or very small change in population size, in an infinitesimal or very small time.

If we focus on the birth and mortality rates, we see that both depend on the number of individuals in the population, for example, the more individuals the population has, the greater number of individuals will be born, the same happens with mortality, so we can define $B$ and $D$ each with a per capita birth and mortality rate:

\(B = bN0\) and \(D = dN0\)

This would leave our equation as follows:

Finally, we can call the factor $b – d$ $r$ or instantaneous population growth rate.

This would be our first equation that indicates an exponential growth of the population. We can notice that at values of r greater than 0 the population grows over time, at values lower it decreases and at value equal to 0 its size is maintained.

To obtain an equation that allows us to project the population into the future we can integrate the previous equation following the rules of calculus, which would give us as a result the following:

This equation allows us to project to a future time our population of paramecia taking into account how many paramecia there are at this moment and their instantaneous growth rate.

Important elements to consider

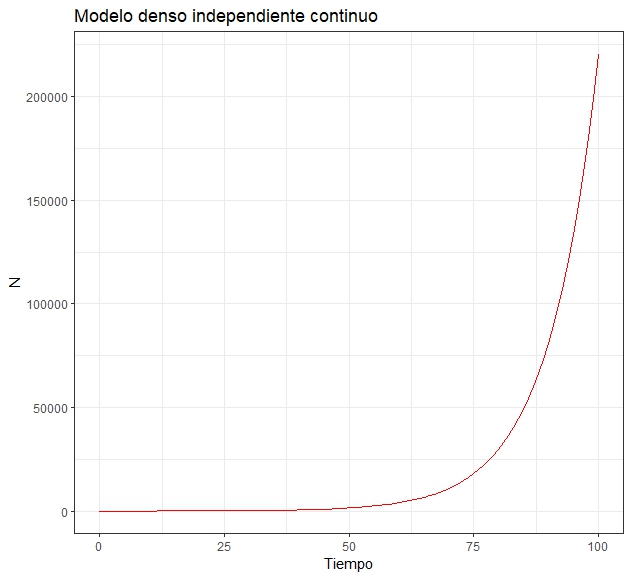
As we have mentioned previously the initial size of the population as well as the growth rate determine the number of individuals in the future changing these parameters we can have different types of curves. But imagine a value of $r$ slightly higher than 0 for our paramecia, something like 0.1 and we project the time in days and starting only with 10 paramecia. In 1 day we would have a new paramecium, in 2 days we would have 2 new paramecia, in 3 days, 3 new ones and so on until reaching the sixth day with 8 new paramecia and a total of 18. Quite slow right? If we continue projecting the population size in a month of 30 days we would have 200 paramecia, but in 100 days we would have more than 220 thousand paramecia. Imagine that these only originated from 10 initial paramecia, so if a population of a species grew this quickly it would populate the entire world, something that in nature does not occur. This model however has the grace of indicating to us the potential that a population of a species could have if there were no restrictions regarding resources. In addition, we can only apply it when certain assumptions are met.

1.- There is no immigration or emigration
2.- $b$ and $d$ are constant parameters, that is to say birth and mortality do not change.
3.- There is no genetic structure, that is to say all organisms have the same reproductive potential and the same associated mortality rate.
4.- There is no age or size structure, all organisms from birth have the same reproductive capacity and associated mortality rate.

Despite how far from reality this model can be, it is usually a key piece from which questions arise such as Why do organisms not grow in this way? What are the conditions for a population to be able to grow exponentially? Relevant questions even in areas related to evolutionary biology. Although you may have read it somewhere, the human population does not grow exponentially, it may be that in some time interval it has been like that, but current data points out that it does not follow that trend, related to the decrease in the growth rate in the last decades. For more information you can check ourworldindata.org.

If you want to delve much more into this topic I recommend the book “a primer for ecology” by Nicholas Gotelli where this type of models is worked in detail.

If this is the first time you face a model of this nature, I leave you the following questions What do you think should be added to this model? What things does it not consider that could be important?